手机访问

游戏资讯

首页 >游戏资讯

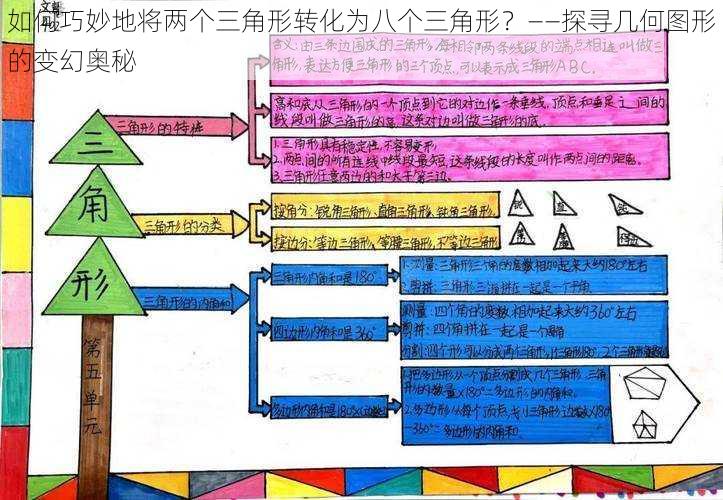
如何巧妙地将两个三角形转化为八个三角形？——探寻几何图形的变幻奥秘

日期： 作者：天堂手游汇 阅读：3

在一个宁静的午后，阳光透过教室的窗户洒在洁白的画纸上。小明坐在画架前，手里拿着一支削得尖尖的铅笔，他的目光中充满了专注和好奇。

“小明，你在画什么呢？”他的朋友小刚好奇地凑了过来。

“我在研究几何图形的变幻呢！”小明兴奋地，“你知道吗？两个三角形可以巧妙地转化为八个三角形！”

如何巧妙地将两个三角形转化为八个三角形？——探寻几何图形的变幻奥秘

小刚听了，不禁感到惊讶：“真的吗？这怎么可能呢？”

小明没有，只是淡淡地笑了笑，继续埋头在他的画纸上描绘着。经过一段时间的努力，他终于完成了他的几何图形转化图。

“看！”小明将画纸举给小刚看，“两个三角形可以通过一系列的变换，变成八个三角形！”

小刚仔细观察着画纸上的图形，不禁感叹：“这真是太神奇了！这其中的原理是什么呢？”

小明解释：“这其实就是几何图形中的拓扑变换。拓扑变换是一种不改变图形形状但可以改变图形大小位置和方向的变化。通过一系列的拓扑变换，我们可以将一个图形转化为另一个图形。”

小刚听了，恍然大悟：“原来这就是拓扑变换的魅力啊！那除了两个三角形可以转化为八个三角形，还有其他有趣的图形转化吗？”

小明点头：“当然有了！比如，一个正方形可以经过一系列变换，变成四个等腰三角形。你看！”说完，他又在画纸上描绘起来。

经过一番努力，小明终于完成了正方形的变换图。

“看！”小明将画纸再次举给小刚看，“一个正方形可以通过一系列的变换，变成四个等腰三角形！”

小刚看着画纸上的图形，不禁感叹：“这真是太神奇了！没想到几何图形中竟然隐藏着这么多有趣的变换！”

小明和小刚一起讨论着这些神奇的图形变换，心中充满了对几何学的热爱和敬畏。他们深深地感叹着：几何图形的世界真是广阔而又奇妙啊！

关键词：

相关资讯